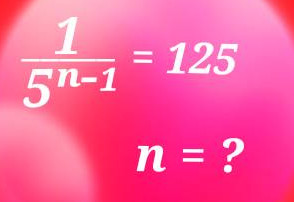
5^-(n-1)=5³
-n+1=3
-n = 3-1
n = -2✓
1/5^n-1 = 125
C.E: notando che la base dell'esponenziale è strettamente positiva e sapendo che una quantità generica elevata a potenza n^x≠0 ∀n≠0 ∧ ∀x∈ℝ, segue che l'equazione è definita in tutto ℝ.
Noto che 125 è riconducibile a base 5 ⇒1/5^n-1 = 1/5^-3
La seguente uguaglianza tra frazioni, avendo i medesimi numeratori, saranno uguali ⇔5^n-1=5^-3 ⇔n-1=-3 ⇔n=-2
osservando che:
5^(-ⁿ+¹)=5³,.... dunque....
–n+1=3,....
n=–2
-->
n =-2
-(-2)+1 =3