(4, 4t+π/2)=(r², -t)
r=2 t=-π/10+2kπ/5
Moltiplica entrambi i membri per z
Ricorda che z per il suo coniugato dà il modulo di z al quadrato
Scrivi z in forma goniometria e sostituisci
L'uguaglianza fra i due membri comporterà una condizione sul modulo di z e una sulla sua anomalia da cui riceverai le soluzioni dell'equazione

Tenendo conto anche del valore del seno, la soluzione per theta diventa 5 theta= π/2+kπ ma con k = dispari.
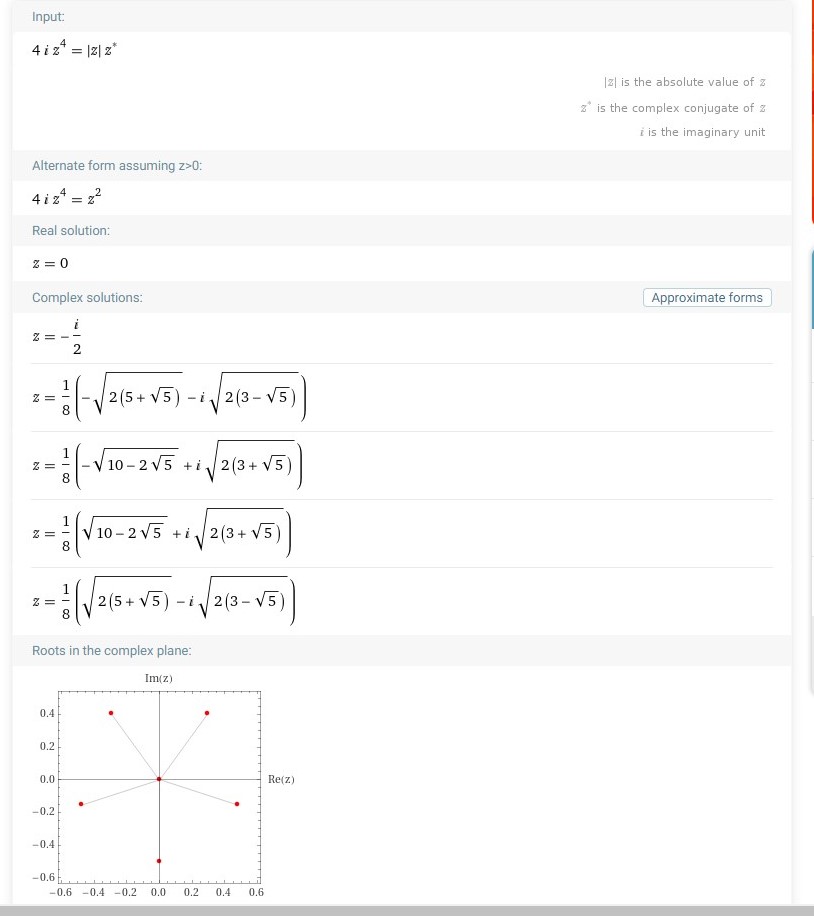
noto innanzitutto che z = 0 è soluz. Dopodiché scrivo z = r · exp(i·theta) e applico il modulo a entrambi i membri => 4 · r⁴ = r · r (perché il coniugato ha lo stesso modulo, r, del numero z non coniugato) => si ottiene r² = 4 · r⁴ e si può dividere per r² (r = 0 corrisponde al numero complesso nullo individuato come soluzione all'inizio). Si arriva dunque a r² = ¼ a cui corrisponde la soluzione r = ½ (r, essendo il modulo, deve essere non negativo, per cui si scarta r = - ½). Ora si deve trovare l'angolo (o fase o argomento): Sostituisco nell'eq. iniz. z = ½ exp(i·theta) trovando 4 · i · (½)⁴ · exp(i · 4 · theta) = (½) · [½ · exp(-i·theta)]. Rielaborando si giunge a exp(-i · theta) = exp(i · [4theta +½π]). Uguagliando gli esponenti e considerando l'intervallo di angoli [0, 2π[ si conclude che gli angoli possibili sono (in numero pari a 5): 3π/10, 7π/10, 11π/10, 3π/2, 19π/10.