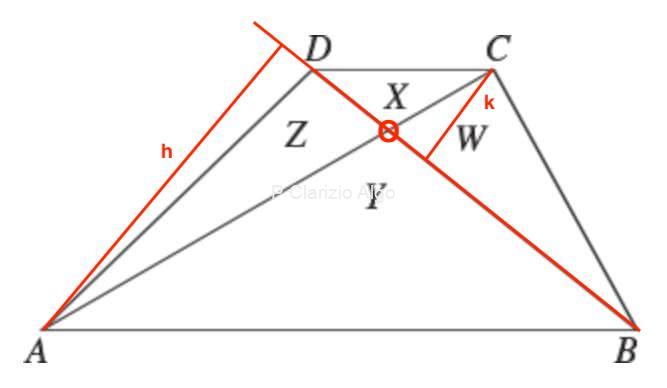
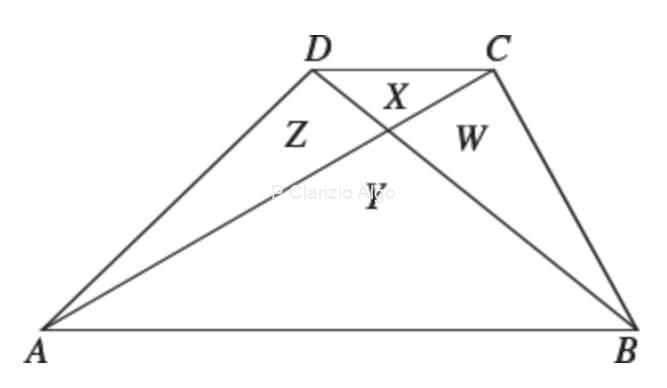
Dato un trapezio ABCD, si traccino le diagonali AC e BD individuando le 4 AREE dei triangoli indicate con X,Y,Z,W
Sussiste la seguente proporzione tra le aree
Z:Y = X:W
PERCHÉ ?
si trova facilmente che i triangoli indicati con X e Y sono simili e che Z=W (perché i triangoli ADB e ABC hanno stessa base ed altezza e quindi Z+Y=W+Y)
chiamo O il punto di intersezione delle diagonali, h l'altezza (comune) dei triangoli AOD e AOB, k l'altezza (comune) dei triangoli DOC e COB.
Allora abbiamo:
Z = OD × h/2;
Y = OB × h/2;
X = OD × k/2;
W = OB × k/2.
Quindi dividendo membro a membro:
Z/Y = OD / OB;
X/W = OD / OB.
E quindi: Z/Y = X/W.