Dato il problema di cauchy: Il problema dato ammette infinite soluzioni
a) Il problema dato ammette infinite soluzioni. (falsa)
(b ) Esiste una soluzione y(x) del problema dato per cui y(π/2) = 0.(falsa)
(c) Ogni soluzione y(x) del problema dato è derivabile. (vera)
Scrivo le risposte per come ho capito io:
(a) falsa perchè il problema proposto ammette una soluzione per c = 0
(b) falsa perchè y(π/2)sin(π/2+2kπ) + c) è 0 per c = -1 ma per infiniti k.
(c) vera perchè y(π/2)=(sin(π/2+2kπ) + c) per ogni k e per ogni c
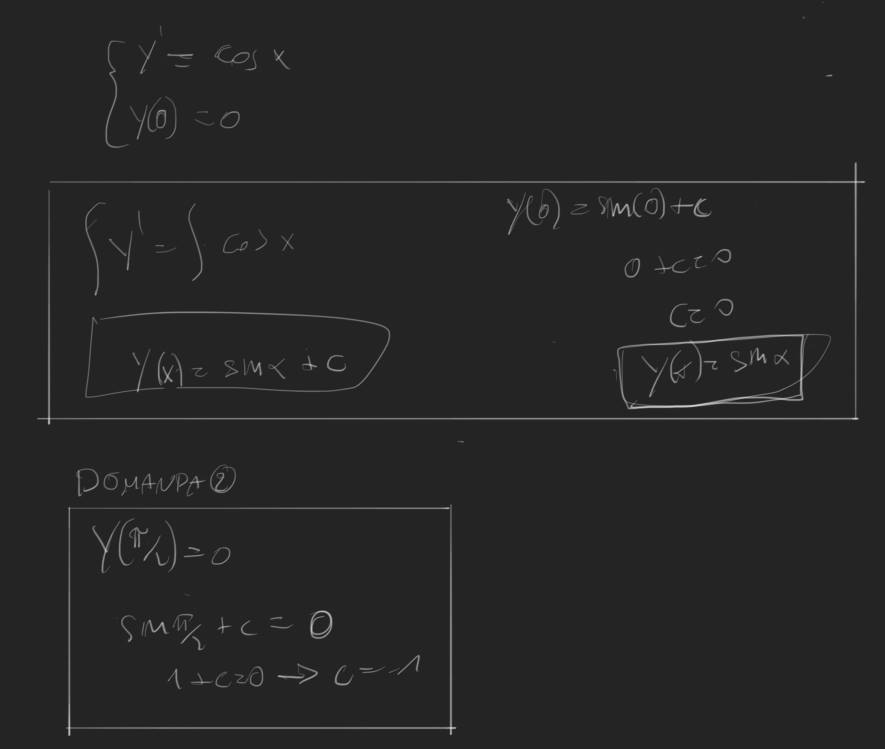
la soluzione dell'equazione differenziale y'(x) = cos(x) è la famiglia di funzioni y(x) = sin(x) + c, con c ∈ ℝ arbitrario. Aggiungendo la condizione y(0) = 0, si ha un problema di Cauchy, che in questo caso determina univocamente c = 0, per cui l'unica soluzione del problema di Cauchy è y(x) = sin(x).
a) Tutto giusto come hai fatto 
b) È giusto anche qui  anche se non occorre ri-determinare c: l'unica soluzione è quella già trovata, y(x) = sin(x), e y(𝜋/2) = sin(𝜋/2) = 1 ≠ 0.
anche se non occorre ri-determinare c: l'unica soluzione è quella già trovata, y(x) = sin(x), e y(𝜋/2) = sin(𝜋/2) = 1 ≠ 0.
"ogni soluzione" corrisponde alla "sola soluzione", cioè y(x) = sin(x), che è una funzione derivabile (cioè ammette derivata) su tutto il suo dominio di definizione ℝ.