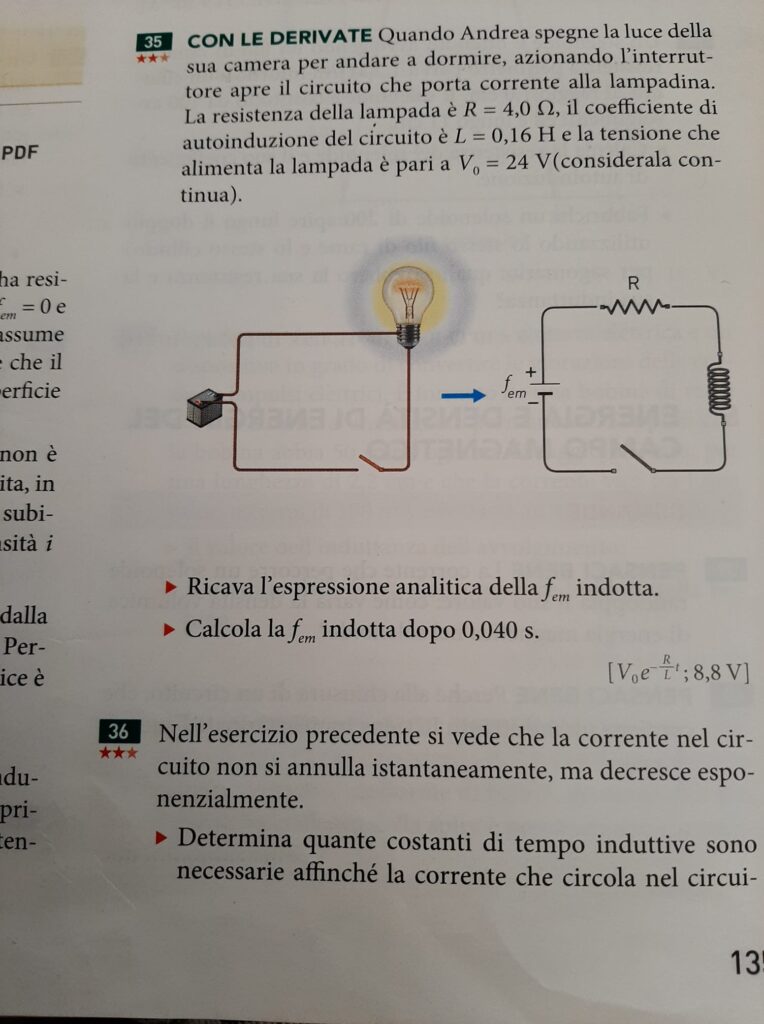
Un circuito è composto da un generatore di tensione V_0 chiuso su di una lampada di resistenza R e induttanza L.

Si supponga che dopo molto tempo il generatore venga cortocircuitato: il circuito equivalente sarà composto da una resistenza R in serie all'induttanza L caricata.

Calcolare la forma analitica della fem ai capi dell'induttore.

La soluzione è la seguente: si consideri la legge di Kirchhoff delle tensioni applicata al circuito in esame. Si ha:

R*i + L*(di/dt) = 0

Dividendo tutto per L si ottiene:

(di/dt) = -(R/L)*i (#1)

ovvero una equazione differenziale con soluzione

i(t) = i(0)*e^[-(R/L)t]

dove i(0) è il valore della corrente all'istante in cui il circuito RL viene chiuso.

La fem è data da:

f_em = -L*(di/dt) = -L*[-(R/L)*i] = R*i(0)*e^[-(R/L)t] (#2)

dove nel secondo passaggio è stata usata la (#1).

Per completare l'esercizio non resta che calcolare i(0), che in questo caso corrisponde alla corrente che circolava nel circuito prima che il generatore fosse cortocircuitato.

Poiché si è supposto che il circuito è rimasto per molto tempo connesso al generatore, esso ha sicuramente raggiunto la condizione di regime, dove l'induttore si comporta come un cortocircuito.

Pertanto:

i(0) = V_0/R

Sostituendo in (#2) il problema è risolto, basta sostituire i dati del problema in:

f_em = V_0*e^[-(R/L)t]

(Nelle formule ho evitato di riportare sempre la dipendenza della corrente dal tempo per non appesantire la notazione, consideri quindi che è i=i(t)).