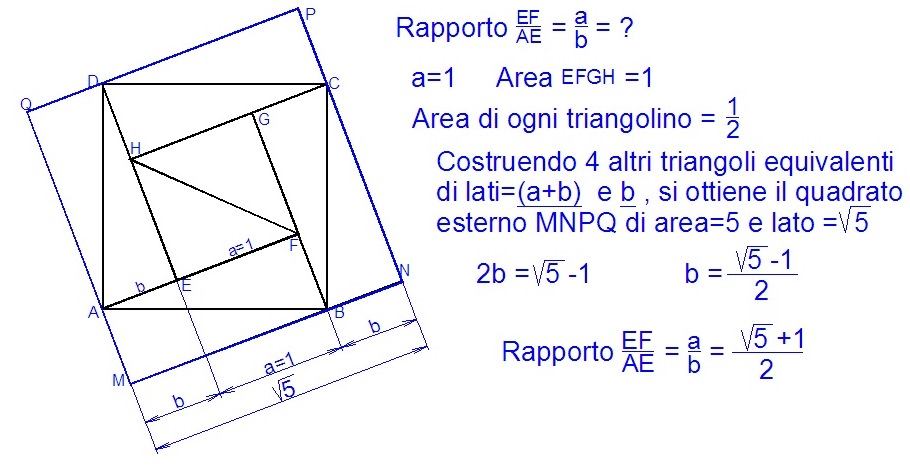
Io trovo EF/AE = 𝜑. Infatti:
Area blu = area marrone
(EF+AE)·FB = EF²
AE·FB·(EF/AE+1) = EF²
EF/AE + 1 = (EF/AE)^2
EF/AE = (1+√5)/2 = 𝜑.
Detto l=AB ciascun Δ ha area=l^2/6 allora il quadrato centrale ha A=3(l^2/6)=l^2/3 ed ogni suo lato EF=l/√3 considerato che i triangoli rettangoli laterali sono uguali,AE =FB allora
(AE+l/√3)^2+AE^2=l^2
6AE^2+2√3AEl-2l^2=0
AE=l(√5-1)√3/6 allora
EF\AE=(√3/3)/(l(√5-1)√3/6)=2/(√5-1)=(√5+1)/2=φ