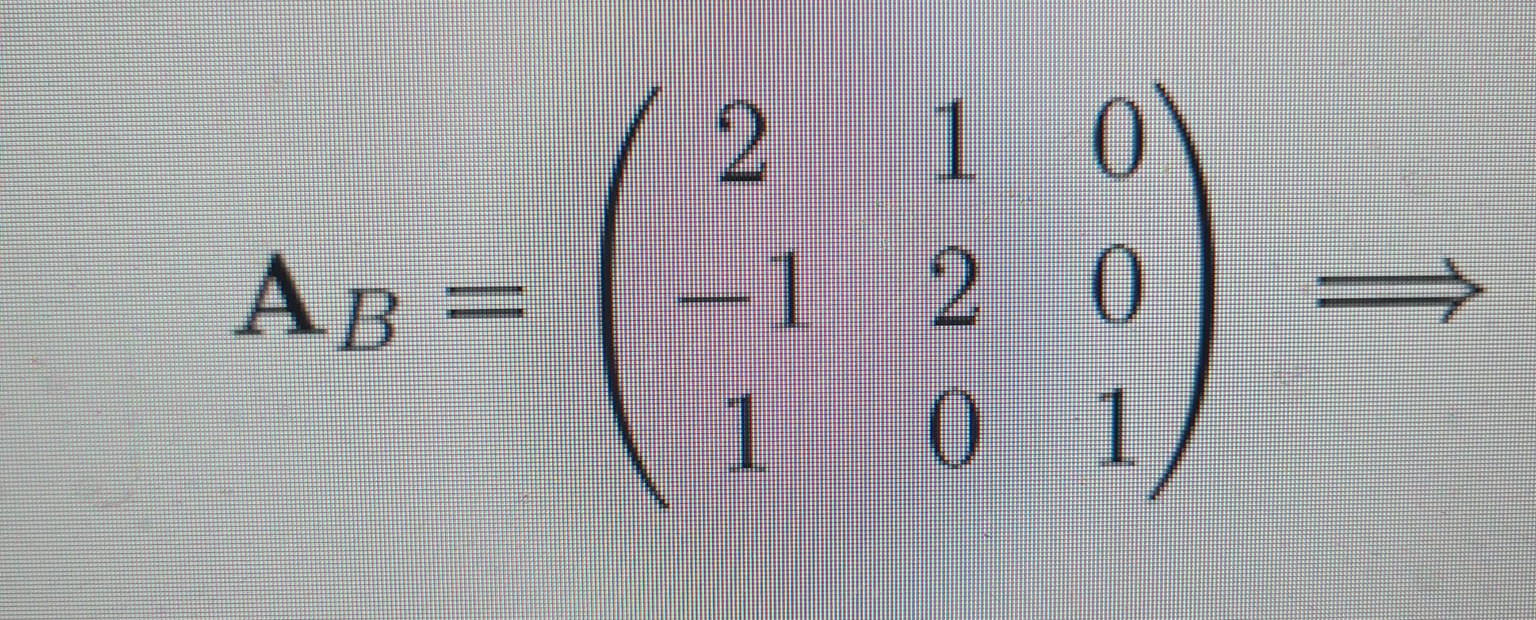
Devo portare questa matrice in forma ridotta tramite Gauss, tuttavia seguendo il procedimento noto che sulla prima colonna è stato fatto perno sul -1 della seconda riga
Devi prima trovare il determinante, poi calcoli l'inversa, se il determinante è positivo, la matrice è invertibile
se il determinante è non nullo
però uno sviluppo di Laplace sull'ultima colonna è più veloce. In verità si vede a occhio senza fare calcoli che il determinante è non nullo: a meno di una costante non nulla il determinante di A coincide col determinante della sua sottomatrice formata dalle prime due righe e colonne, e le prime due righe sono non proporzionali quindi indipendenti.
il mio lavoro è un altro, personalmente preferisco Sarrus, l'ho utilizzato ampiamente anche in Ricerca Operativa, per matrici nxn di dimensioni ridotte