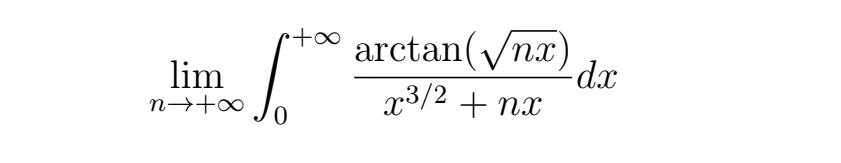
La funzione tende puntualmente a 0 ed è dominata da g(x) con g(x)=1/rad(x) per 0<x<1 e g(x)=π/(2x^(3/2)) per x>=1
Ho bisogno di una funzione integrabile da 0 a +oo che domina l'integranda, in modo da poter utilizzare il Teorema della Convergenza Dominata. Da 0 a 1 tengo solo il nx nel denominatore, uso il fatto che arctan(x)<x e assumo n>1. In questo modo ottengo la 1/x^(1/2), integrabile da 0 a 1. Per x>1 tengo solo il x^(3/2) nel denominatore e uso il fatto che arctan(x)<π/2, ottenendo la seconda parte (integrabile). Per maggiori informazioni dai un'occhiata al Teorema della Convergenza Dominata, è uno strumento formidabile.