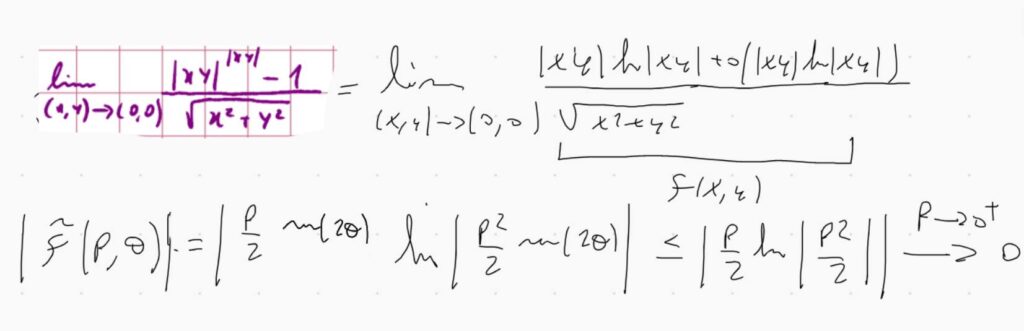Se (x,y)->(0,0) anche |xy|->0
Scrivo |xy|^|xy| come exp(log(...))
E dato che |xy|^|xy| tende a 1 il logaritmo tende a 0 e quindi posso sviluppare l'esponenziale in serie attorno a zero e viene
(|xy|^|xy|-1)/sqrt(x²+y²)=|xy|log|xy|/sqrt(x²+y²) + ordini superiori
che in coordinate polari è
r|sin(a)cos(a)| log(r² |sin(a)cos(a)|)
Togliendo le divergenze quando si avvicina agli assi (che sono già fuori dal dominio di esistenza e che corrispondo a sin(a)cos(a)=0) posso dire che fa 0