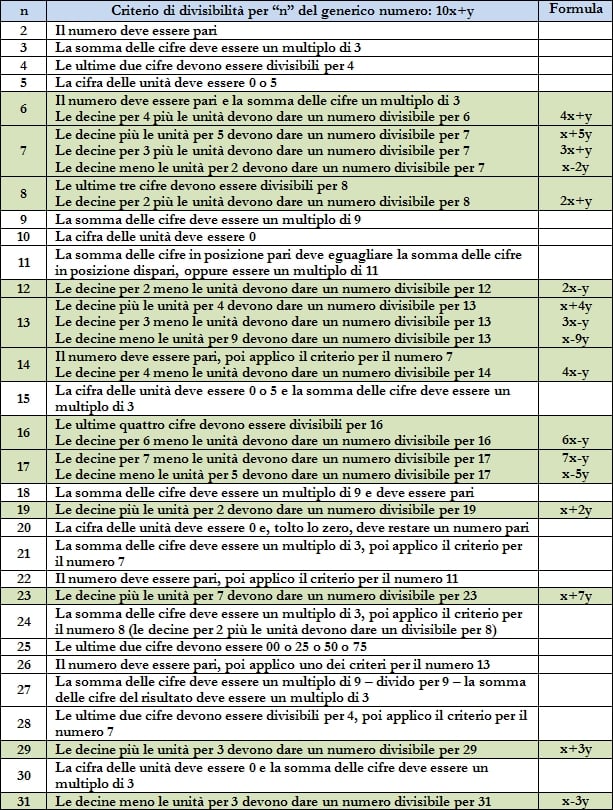
Non tutti sanno che è possibile stabilire a mente se un numero di tre o quattro cifre è divisibile per 7. Un numero qualsiasi può essere indicato come 10x + y. Il simbolo della moltiplicazione, in matematica, si omette. Per capire se un numero del genere è divisibile per 7, basta ridurlo tramite questa formula:

x + 5y

Se il numero così ottenuto è divisibile per 7, allora lo era anche l’altro. E il procedimento può essere ripetuto fino a ottenere un numero piccolo, che è facile stabilire se è divisibile per 7.

Proviamo ad applicare la formula al numero 252 (x è 25 e y è 2):

25+5*2=35 (divisibile per 7, per cui lo è anche 252)

Proviamo ora col numero 413:

41+5*3=56 (divisibile per 7, per cui lo è anche 413)

Proviamo ad applicarla al numero 665:

66+5*5=91 => 9+5*1=14 (divisibile per 7, per cui lo è anche 665)

Il procedimento di riduzione può essere usato più volte, finché non si ottiene un numero piccolo.

Proviamo ad applicarla al numero 1234:

123+5*4=143 => 14+5*3=29 (NON è divisibile per 7, per cui non lo è nemmeno 1234)

Proviamo ora col numero 2471:

247+5*1=252 => 25+5*2=35 (divisibile per 7, per cui lo è anche 2471)

E se volessimo stabilire se un numero è divisibile per 13? Si deve usare una formula simile.

x + 4y

Proviamo il criterio di divisibilità per 13 con il numero 403:

40+4*3=52 => 5+4*2=13 (divisibile per 13, per cui lo è anche 403)

Proviamo ad applicarla al numero 1274:

127+4*4=143 => 14+4*3=26 (divisibile per 13, per cui lo è anche 1274)

Proviamo ad applicarla al numero 2523:

252+4*3=264 => 26+4*4=42 => 4+4*2=12 (NON è divisibile per 13, per cui non lo è 2523)