L’ignota disciplina dei numeri naturali che regola la distribuzione dei numeri primi - (II)
Congettura di Oppermann
Nell’anno 1882, Ludwig Oppermann, analizzando fra i numeri naturali il percorso dei numeri primi notò la loro costante doppia presenza fra ciascun quadrato perfetto e il suo successivo e quindi presunse che tra n(n – 1) e n^2 vi è sempre almeno un numero primo e almeno un altro tra n^2 ed n(n + 1). Della veridicità di tale congettura, finora non dimostrata ne confutata da alcuno, se ne illustrano, nei paragrafi successivi, le articolate motivazioni suffragate dal fenomeno matematico delle “confluenze” e delle “repliche” dei divisori Mm che sono causa di sempre più presenze di numeri primi all’interno delle stanze quadratiche. Infatti, le chiavi che consentono l’accesso all’apertura del libro della Natura che contiene la legge matematica che regola la distribuzione dei numeri primi sono due:
La prima chiave consente di individuare all’interno dell’ordine della sequenza dei numeri naturali che partendo dal numero 1 viaggia verso l’infinito una serie, anch’essa infinita, di sotto ordini costituiti da coppie di intervalli numerici definiti stanze quadratiche A e B.
Definizione di stanze quadratiche
Attribuendo a n il valore di ciascun numero naturale, si definiscono “stanze quadratiche A” tutti gli intervalli, limitati e chiusi, [n(n-1)+1, n^2]; si definiscono “stanze quadratiche B” gli intervalli, limitati e chiusi, [(n^2+1), n(n+1)].
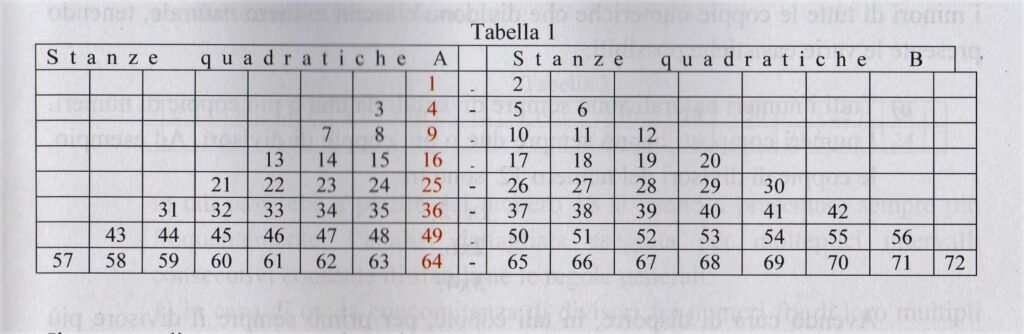
Il nome di stanze quadratiche trae origine dal fatto che l’ultimo elemento dell’intervallo A (vedere tabella 1) è sempre costituito da un quadrato perfetto (1, 4, 9, 16, 25, ecc.) mentre quelli della stanza B sono costituiti dagli elementi immediatamente successivi al quadrato perfetto, fino al successivo numero planico, cioè il numero prodotto di n(n+1). La quantità degli elementi che compongono le stanze quadratiche A e B è sempre fra loro uguale. Se la stanza quadratica A ne contiene due, anche la stanza B ne contiene due. Se la stanza quadratica A ne contiene tre anche la stanza B ne contiene tre. Se la stanza quadratica A ne contiene mille anche la stanza B ne contiene mille. La quantità degli elementi delle stanze quadratiche A e B corrisponde sempre alla radice del quadrato perfetto di riferimento. La caratteristica comune di tali coppie A e B di stanze quadratiche è, così come congetturò Ludvig Oppermann, la costante presenza dei numeri primi all’interno di ciascuna di esse.
La prima coppia di stanze quadratiche è costituita dal numero 1, per la stanza A, e dal numero 2 per la stanza B. Un solo elemento per ciascuna stanza in quanto la radice del quadrato perfetto di riferimento 1 è uguale a 1. La seconda coppia della serie è rispettivamente costituita dai numeri 3 e 4 per la stanza A e dai numeri 5 e 6 per la stanza B. Due soli elementi per ciascuna stanza in quanto la radice del quadrato perfetto di riferimento (che è il 4, quadrato perfetto del 2) è uguale a 2. La terza coppia della serie è rispettivamente costituita dai numeri a seguire, cioè 7, 8, 9 per la stanza A e dai numeri 10, 11, 12 per la stanza B. Tre soli elementi per ciascuna stanza in quanto la radice del quadrato perfetto di riferimento 9 è uguale a 3. La quarta coppia di Stanze quadratiche della serie è rispettivamente costituita dai numeri a seguire, cioè 13, 14, 15, 16 per la stanza A e dai numeri 17, 18, 19, 20 per la stanza B. Quattro elementi per ciascuna stanza in quanto la radice del quadrato perfetto di riferimento 16 è uguale a 4. La quinta coppia di stanze quadratiche A e B è rispettivamente costituita dai numeri 21, 22, 23 ,24, 25 per la stanza A e dai numeri 26, 27, 28, 29, 30, per la stanza B. Cinque elementi per ciascuna stanza in quanto la radice del quadrato perfetto di riferimento 25 è uguale a 5. E così via, all’infinito.
Prossimo ovvio passaggio è la descrizione e le caratteristiche dei divisori Mm i quali ovviamente non sono “nuovi” divisori bensì un particolare divisore in dotazione di ciascun numero naturale intero e positivo, di volta in volta selezionato con criteri comuni a tutti gli altri e quindi facilmente individuabili anche fra i molti divisori che determinati numeri composti hanno (i numeri composti del 24, ad esempio, sono 1, 2, 3, 4, 6, 8, 12, 24, tuttavia il naturale divisore di 24 è solo uno di essi individuato col criterio che la natura ha fissato).