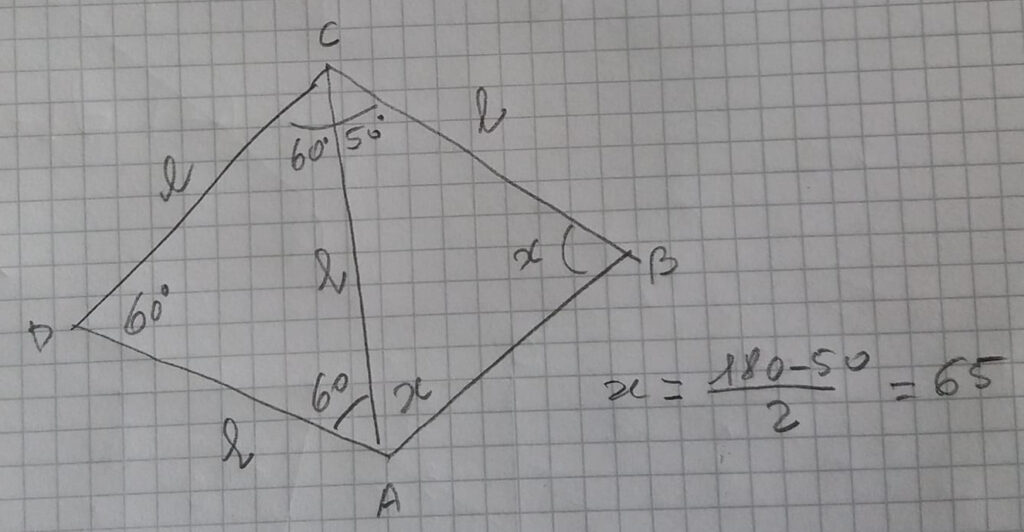
Dividiamo il quadrilatero in due triangoli di cui uno equilatero e l'altro isoscele; quest'ultimo ha l'angolo al vertice C^=50° e ciascuno degli angoli alla base (A^=B^=x°) =65°
Il quadrilatero si divide in due triangoli, uno equilatero e uno isoscele con l'angolo al vertice pari a 50°, quindi gli altri due pari ad X valgono 65°
AC=l perché ACD è equilatero, quindi il triangolo ACB è isoscele per cui 180°-50°=130° e X°=130°/2=65°

Il triangolo ADC non è solo isoscele, ma anche equilatero, perché essendo isoscele per ipotesi, allora gli angoli alla base sono uguali, che sono uguali anche loro a 60 gradi. Per cui la congiungente AC è pari al lato L.
Quindi anche ACB è isoscele e l’ angolo al vertice è 110 gradi meno 60 gradi, cioè 50 gradi.
Quindi quelli alla base, essendo uguali, sono pari a 180 gradi meno 50 gradi e il risultato diviso due, cioè 65 gradi.
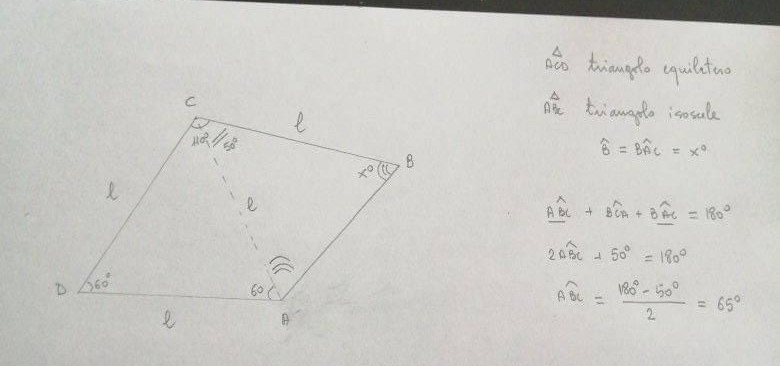
angolo ACB =50°; triangolo ACB isoscele con base AB; CAB=CBA=65°