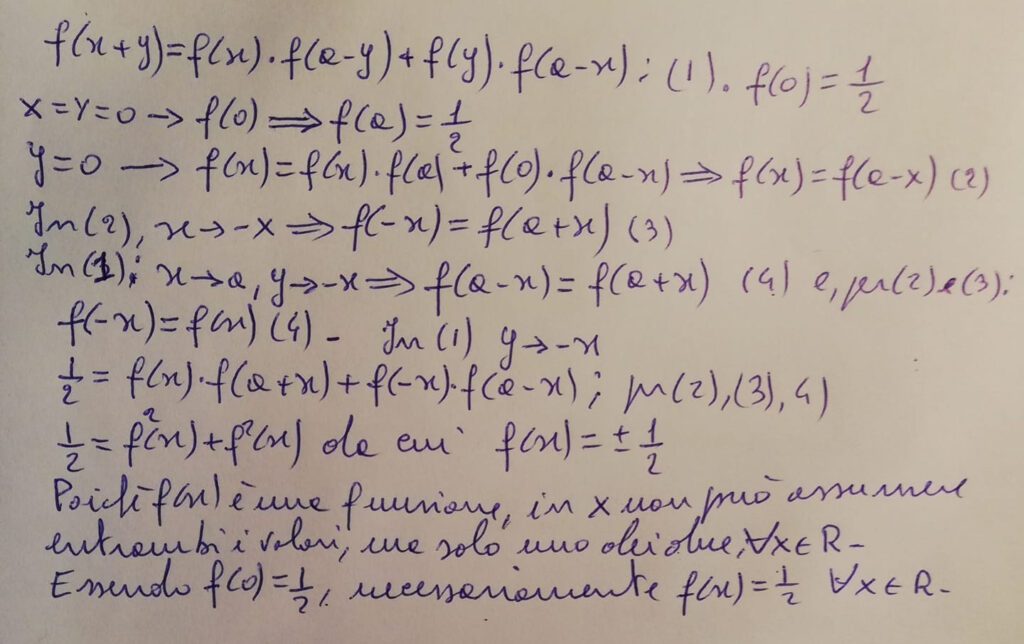È data la funzione f: R --> R con le proprietà
1) f(x + y) = f(x)f(a - y) + f(y)f(a - x)
con x, y reali arbitrari e a reale fissato;
2) f(0) = 1/2.
Calcolare l'integrale definito da meno pi greco a più pi greco di f(x).
Si dimostra che f(a)=f(0)=1/2 e, quindi, che f(a-x)=f(x), f(a-y)=f(y). Dunque la funzione f verifica l'equazione di secondo grado (f(x))^2-f(x)+1/4=0, che è verificata da f(x)=1/2 ∀x ∈ R. Quindi l'integrale vale esattamente pi greco.
se dimostrassimo:
Per i particolari si osserva che, dalla definizione della funzione f, ponendo x=y=0, si ottiene f(0)=2f(0)f(a), da cui, essendo f(0)=1/2, si ha: f(a)=f(0)=1/2. Detto ciò, ponendo y=0 nella definizione di f, si ha f(x)=f(x)f(a)+f(0)f(a-x)=f(x)(1/2)+(1/2)f(a-x), da cui (1/2)f(x)=(1/2)f(a-x), ovvero f(x)=f(a-x). In modo del tutto analogo si ottiene f(y)=f(a-y). Quindi, tornando alla definizione di f, si ha f(x+y)=(f(x))^2+(f(y))^2. Allora, ponendo ad esempio y=0, si fa f(x)=(f(x))^2+(f(0))^2 e, quindi, (f(x))^2-f(x)+1/4=0.