Frattale col Metodo di Newton
il metodo delle tangenti di Newton e il mondo dei frattali
il metodo di Newton è un algoritmo iterativo che può essere benissimo sfruttato nel piano complesso per creare molte immagini suggestive di frattali.
L'idea di fondo è quella di applicare il metodo di Newton alla funzione complessa f(z) = z^p + 1 sui punti complessi della figura che identificano la posizione centrale dei vari pixel e rappresentare la loro 'velocità di convergenza' mediante una scala di colori predefinita.
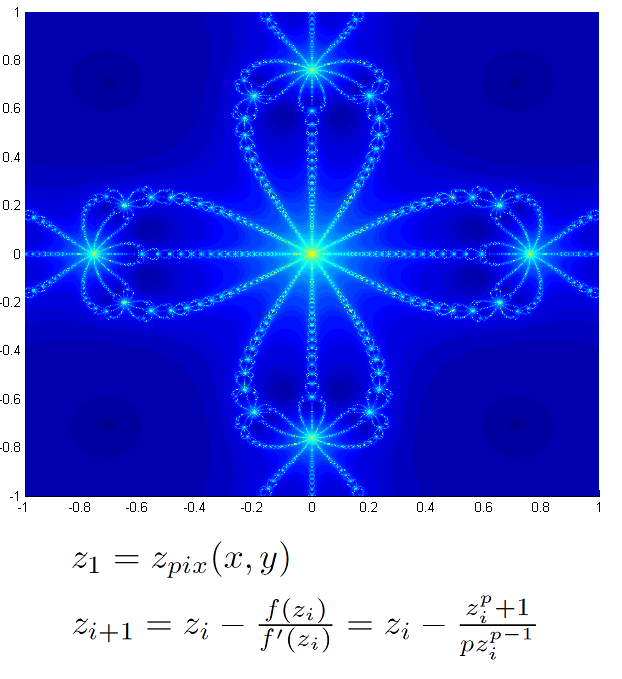
quando il metodo converge rapidamente e zone giallo/verde scargianti quando impiega in proporzione più iterazioni per convergere.
La posizione di ogni pixel è dunque rappresentata dal numero complesso z0 = pixel(x,y) che fornisce il valore di innesco del metodo. La condizione di arresto dell'algoritmo di solito può essere effettuata mediante due test in successione:
1. si richiede che la distanza tra due termini z(i) e z(i-1) appartenenti ad una stessa successione non superi una certa tolleranza piccola decisa dall'utente: |z(i)-z(i-1)| < toll
2. si richiede di fissare preventivamente un numero massimo di iterazioni superato il quale si ritiene che il metodo non arrivi a convergenza (ad esempio Nmax = 255 per una scala di colori a 256 livelli).