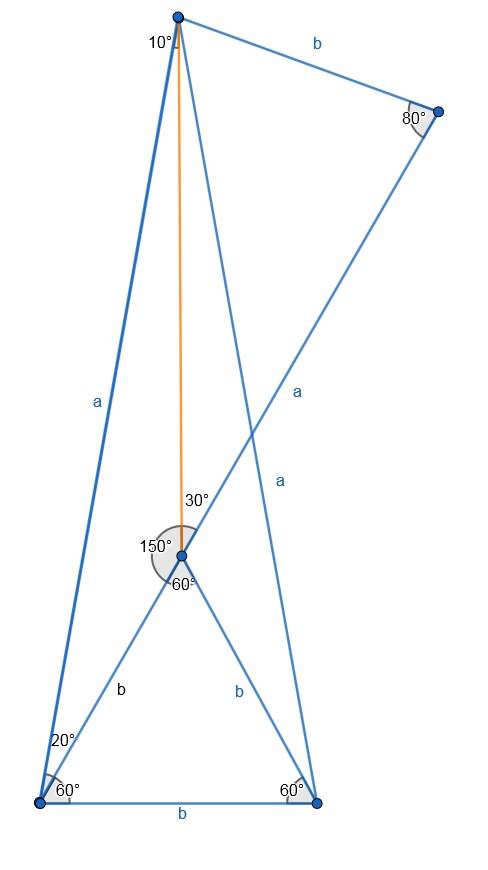
Dapprima si costruisca il triangolo equilatero ACC1, triplicando la dimensione del lato AC.
I suoi angoli saranno, per definizione, di 60 gradi ciascuno.
Poi si focalizzi l'attenzione sul triangolo B1CC1, che è isoscele, poichè AC = C1C = B1C.
Di quest'ultimo triangolo, conosciamo l'angolo in C, che sarà pari a 60-20=40 gradi.
Gli altri 2 angoli di un isoscele sono uguali, per cui (180-40)/2 = 70 gradi ciascuno.
Ora, sviluppando i calcoli sugli angoli sulla base dei dati acquisiti, determiniamo che ABC e AB1C1 sono congruenti, poichè due dei loro lati in comune sono noti ed hanno gli stessi angoli.
Ora è facile determinare che l'angolo ignoto sarà pari a 30 gradi.
A-B1 e B-C sono dati uguali dal problema nell'enunciato.
A-C e A-C1 sono uguali altresì, poichè sono lati del triangolo equilatero costruito su A-C dato.
La congruenza di ABC e AB1C1 vien poi sancita dal calcolo sugli angoli: sia gli angoli in A e in B1 sono pari a 80 gradi (dall'enunciato iniziale: uno è dato a 80 gradi, l'altro è ovviamente identico, poichè 180-(80-20)=80).
Se aggiungi ora il ragionamento che ne deriva, vedrai che i due triangoli in oggetto non possono essere che congruenti (hanno gli stessi angoli e 2 lati comuni sono noti).
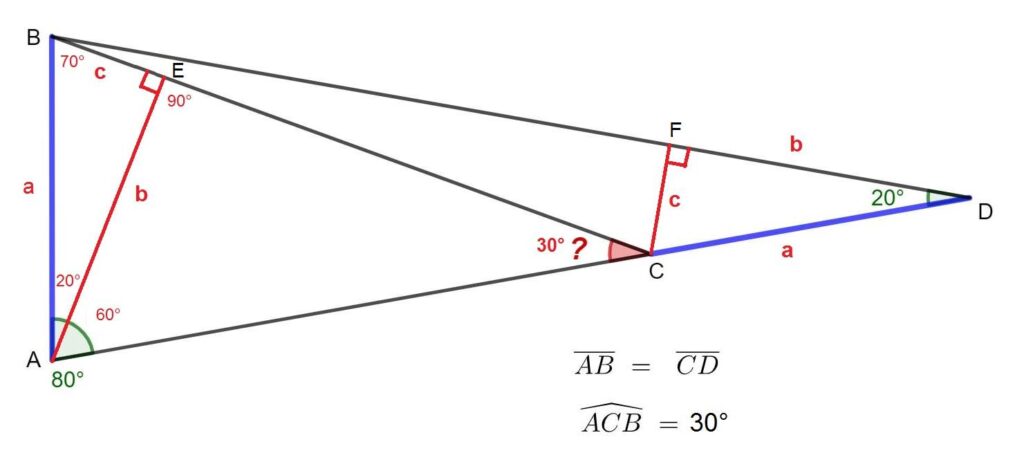
ABE è congruente a CDF