
Ci potrebbe essere una possibilità: il punto D é il punto di intersezione tra una retta con coefficiente angolare tg (65) e passante per 0,0 e una retta di inclinazione tg (45) e passante per 100,150. Da qui trovo le formule delle rette.
Mettendo tali rette a sistema trovo le coordinate del punto D (in un sistema di riferimento centrato in C). La lunghezza di DE coincide con la Y del punto
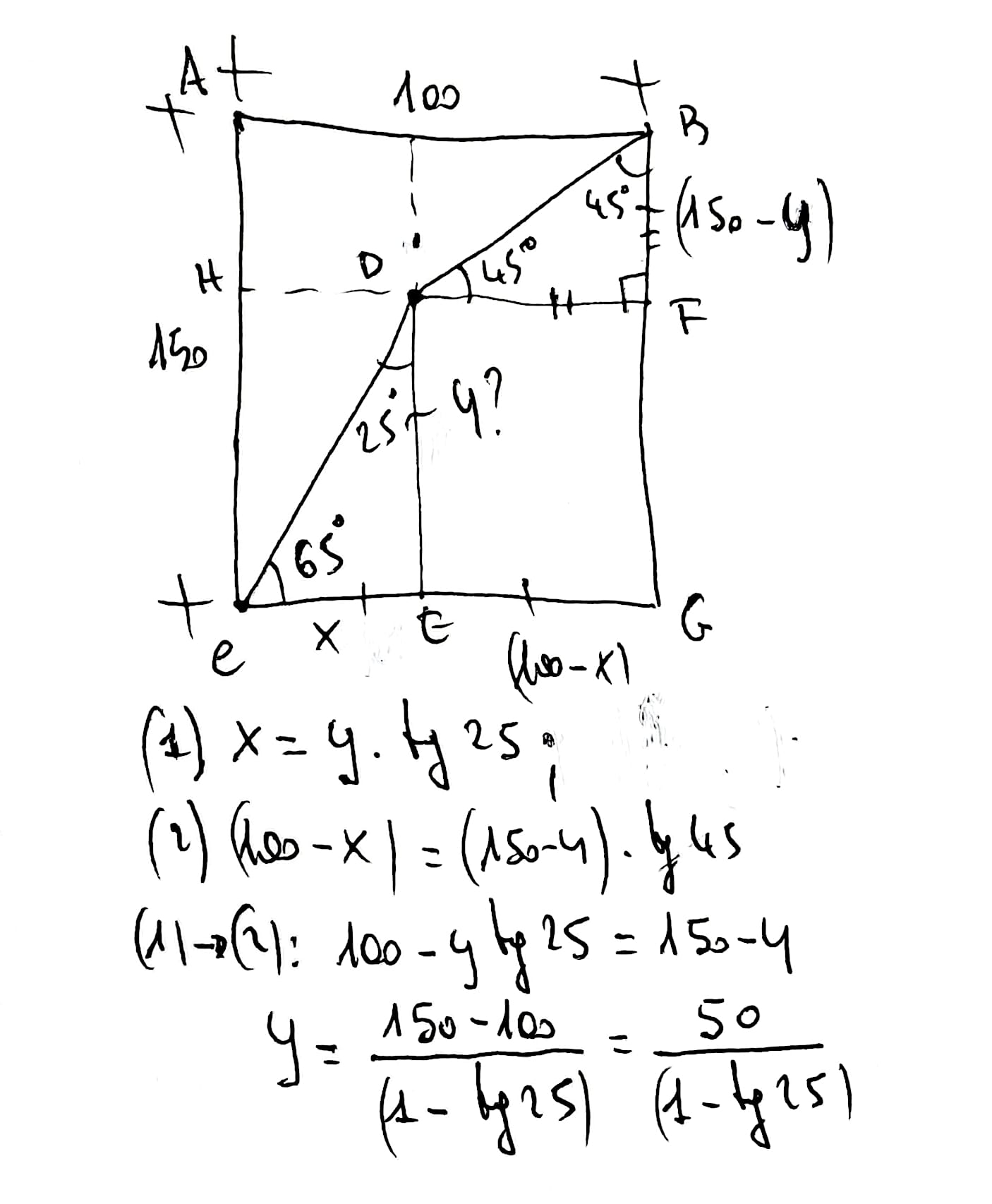
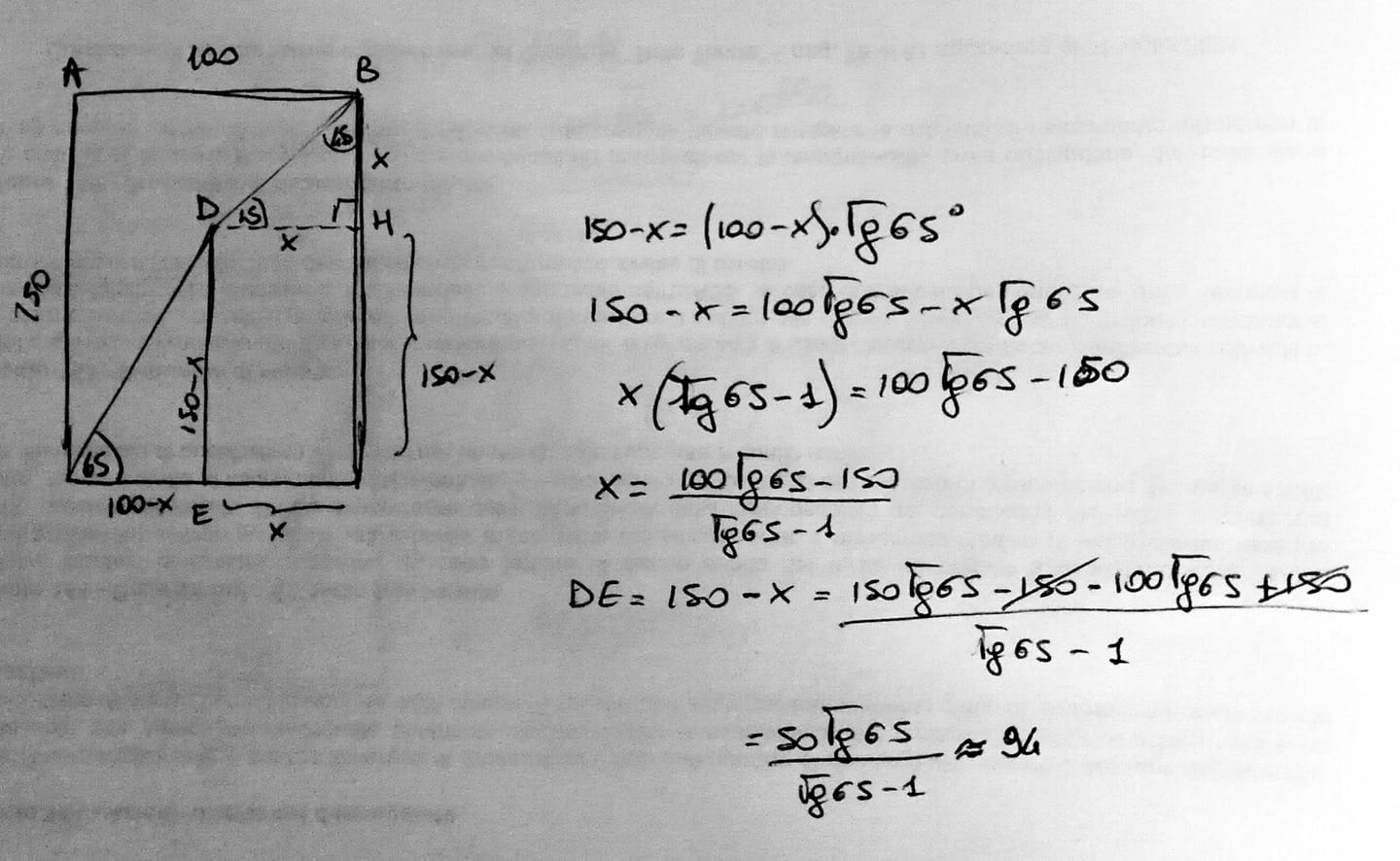
A- trigonometria e geometria
Poni DE=x; trova quindi, subito, FG, EG, BF e DF in funzione di x.
Trova anche CE=xtan25°.
Somma CE+EG e imponi che il risultato sia 100; trovi così x, che è il valore cercato, come:
50/(1-tan25°).
B- geometria analitica
Poni assi cartesiani sui lati inf e sx, con Origine in C.
Trova le rette: r, per C,D; ed s, per D, B, rispettivamente.
r: y=xtan65°
s: y=x+50
Trova il punto di contatto, E, col sistema delle 2 equazioni sopra; stavolta però, è la y che ti serve, in quanto ordinata di E, ed esce:
y= (50tan65°)/(tan65°-1)
In entrambi i casi il valore è lo stesso, ed è circa 93.7 .