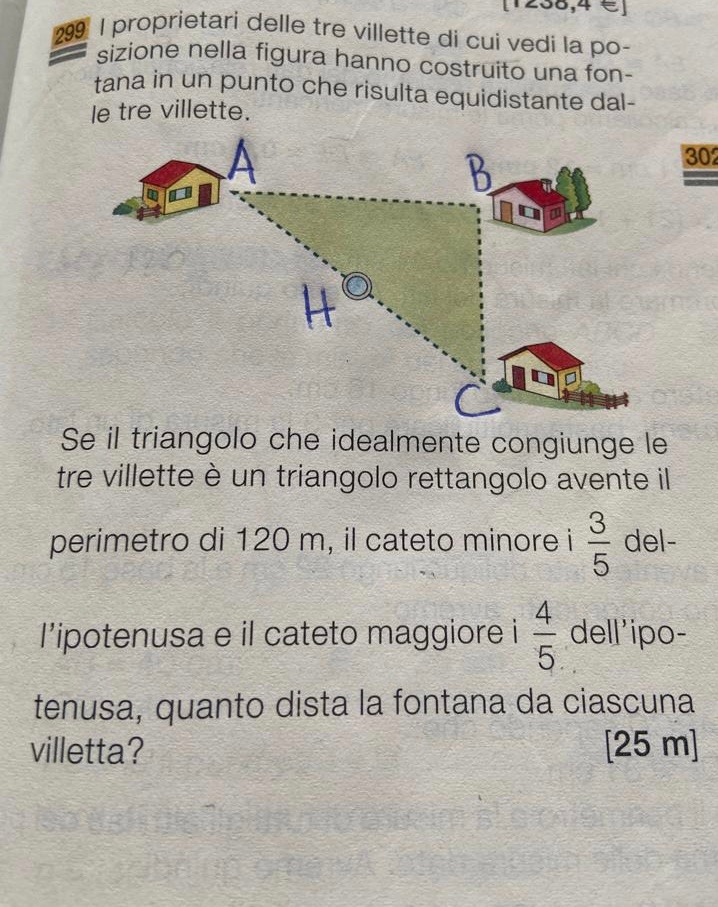
se il triangolo che idealmente congiunge le tre villette è un triangolo rettangolo

Abbiamo risolto con questo ragionamento:
BC 3/5
AB 4/5
CA 5/5
120:12=10
BC 30
AB 40
CA 50

Quando però andiamo a calcolare BH, succede che:
Area: 30*40:2= 600
Formula inversa per trovare BH:
600*2=1200:50= 24

l'errore, potrebbe esser questo:

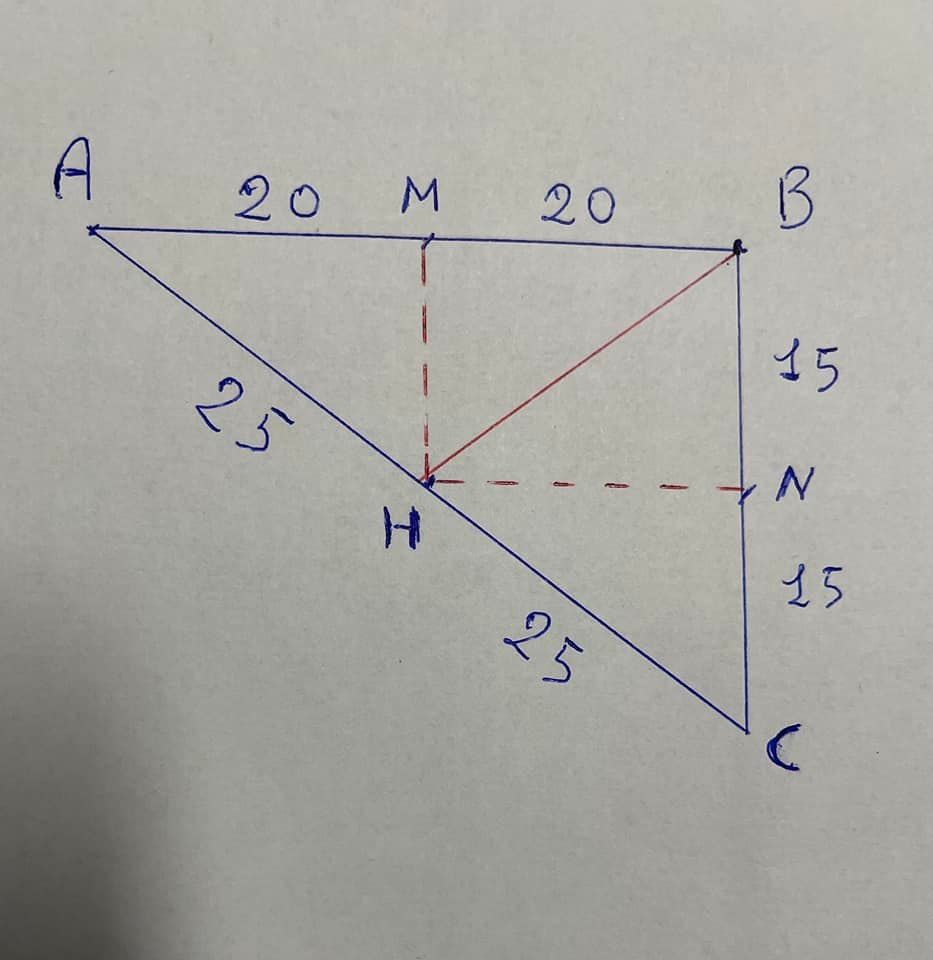
H non è il piede dell'altezza del triangolo, rispetto alla base AC. Ecco dove si trova l'errore. AH = HC = 25. Il triangolo ABC è inscritto in una circonferenza di diametro AC.

HB non è l'altezza relativa all'ipotenusa .Quella che hai calcolato giustamente vale 24 ma non coincide con il segmento HB

pensandoci anche:

Puoi calcolare BH con Pitagora visto che H é il punto medio di AC le due perpendicolari passano per i punti medi dei cateti Si potrebbe usare anche teorema triangolo rettangolo inscritto