Calcolare l’ESATTA misura della superficie del laghetto.
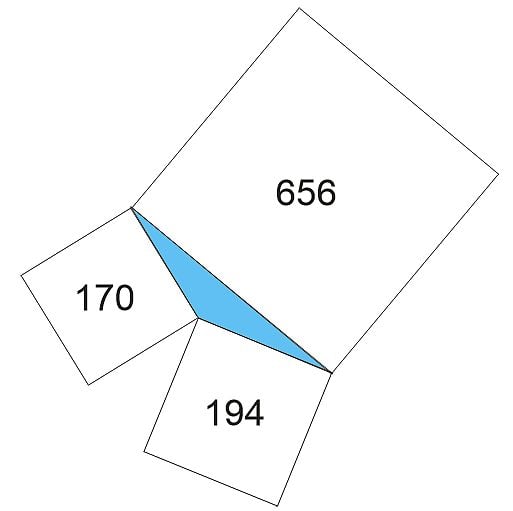
Formula di Qin Jushao.
Area=(1/2)*sqrt(a2*c2-((a2+c2-b2)/2)^2)
con:
a2=656; b2=194; c2=170;
Area = 54
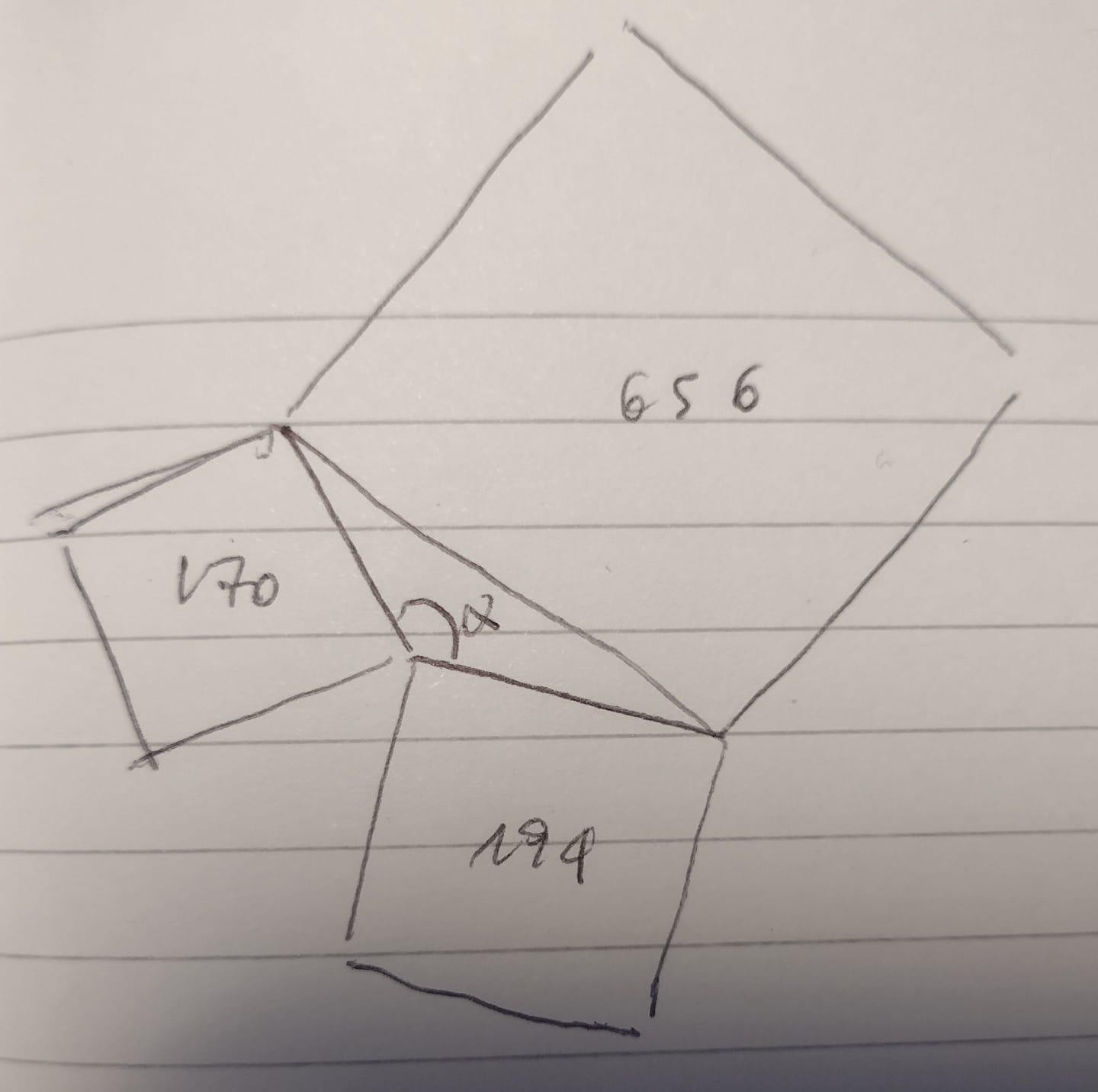
Detto α l′angolo ottuso di lati i quadrati 170 e 194
uso Carnot e poi area parallelogramma diviso 2.
656=170+194-2√(170·194)cos(α)
da cui
cos(α)=-73/√(8245)
sin(α)=√(1-cos²(α))
sin(α)=54/√(8245)
Atr=√170√194sin(α)/2
Atr=2√(8245)·54/(2√(8245))
Atr=54
Notando che le tre aree sono tutte esprimibili come somme di 2 quadrati (170=7²+11², 194=5²+13², 656=16²+20²) possiamo ridisegnare il problema come in figura, dove l’area da trovare si calcola semplicemente sottraendo dall’area dell’intero triangolo: 16*20/2=160, le tre aree esterne al lago: 38,5+32,5+35=106. 160-106=54
È meglio usare la formula risolutiva dell' antico matematico Cinese Qin Jiushao, almeno con i radicali?
A≠√[(a²+b²+c²)²–2(a⁴+b⁴+c⁴)]/4=54