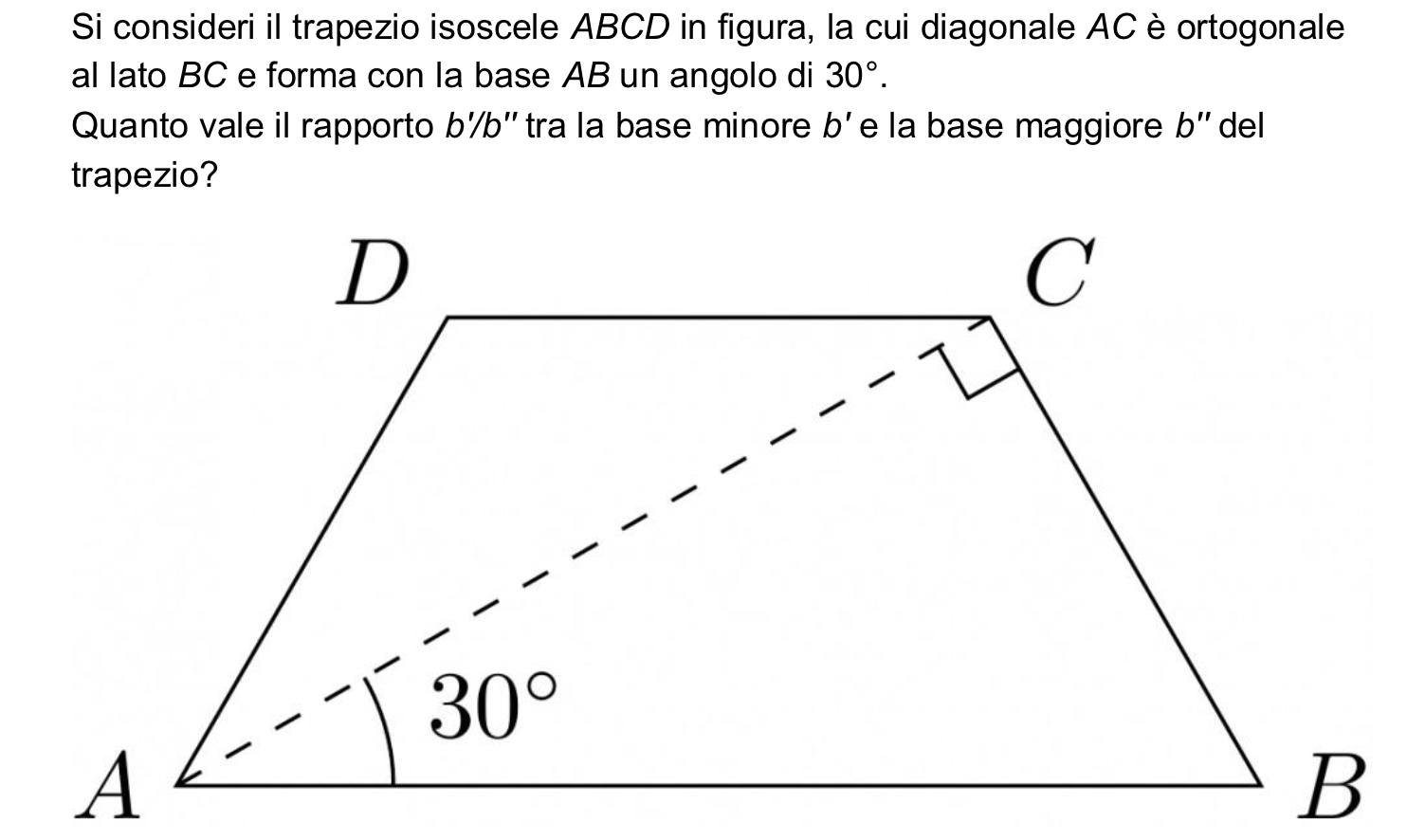
Il trapezio si puo inscrivere in una semicirconferenza .poi disegna l'angolo al centro corrispondente all'angolo alla circonferenza di 30 gradi.
Si può anche risolvere o con la trigonometria oppure sfruttando il fatto che nel triangolo ABC i due angoli complementari sono di 30 e 60 gradi per cui BC=AB/2 poi considerando il triangolo che si forma tracciando l'altezza il cateto minore HB=CB/4 da qui ricavi che DC=AB-2HB=1/2AB
Considero triangolo ABC: l’angolo B misura 60 gradi ( 180-90-30). Il trapezio è isoscele quindi angoli A =B=60gradi e di conseguenza D=C=(360-60-60)/2=120. Gli angoli DAC e DCA sono congruenti e misurano 30 gradi quindi il triangolo DAC è isoscele e DC=AD. Tracciando le altezze DH e Dc si formano due triangoli rettangoli, congruenti con angoli di 30-60 gradi: AH =1/2DA BH=1/2CB. AB =1/2+1+1/2=2 ( due volte DC. Base minore è la metà della base maggiore