La funzione Z di Reimann 1/n^s evoluzione di quella di Eulero della progressione armonica di Basilea
posiziona i numeri primi sul piano, le parti divisibili per due si annullano giustificando nell'intero il numero primo. Nella compensazione fra parte chiamata reale e l'altra irreale (perché l'una simmetrica all'altra con l'asse critico passante fra i due nel centro) c'è lo zero banale. Gli zeri non banali si trovano sull'intersezione fra una sequenza successiva e la precedente non passante sull'asse critico
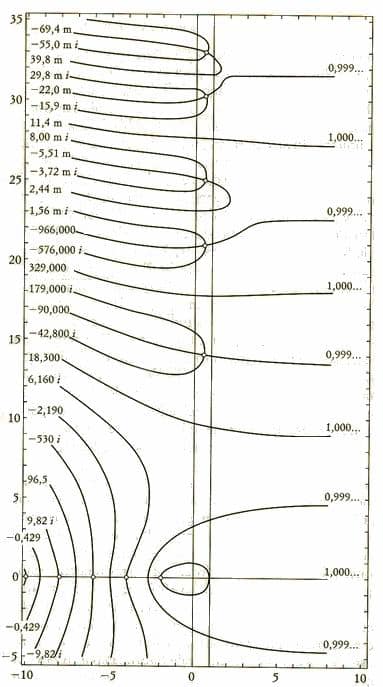
Oppure hanno cercato di dare una forma una chiusura al piano dimensionale che si genera con la gravità. Ponendo la verticale come altezza e il piano bidimensionale come cateto abbiamo un triangolo isoscele. La verticale come asse y la base x. Ricercando l'equilibrio la parte sx deve essere uguale ma di segno inverso alla dx. Nella f z numeri irreali e reali. Affinché non perdiamo l'equilibrio il numero 1 deve essere isolato e lo è se solo se sx = - dx. Se non lo è lo sarà con la progressione armonica e non armonica 1/n^s affidandosi ai numeri che sono il movimento dell'universo. (Spiegarmi non è facile...credo che la funzione z sia nata per individuare i numeri primi nella bidimensione per potersi orientare con la gravità la verticale)