
dato che logx tende a infinito al tendere della x a infinito, allora infinito /infinito più 2 alla infinito =forma indeterminata. Per sciogliere l indeterminazione si ponga log x uguale a y l espressione diviene (y/2+y)alla y con y che tende a infinito,, bene y/y+2= 1-2/y+2 quindi (1-2/y+2) alla y, quindi si arriva a e alla-2y/y+2 che al tendere ad infinito fa -2 quindi e alla meno due.
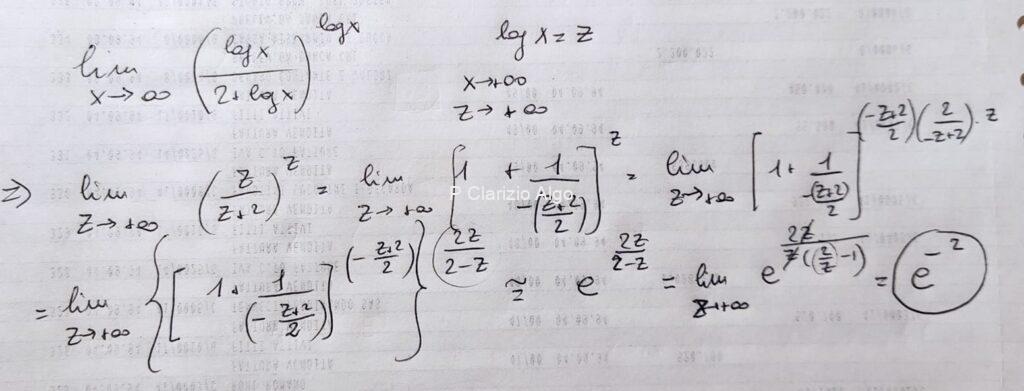
E' il secondo dei due limiti notevoli:
lim x-> ∞ ((x+a)/x)^x=e^a
lim x-> ∞ ((x/(x+a))^x=e^-a
quindi il limite risulta, con a=2:
lim=e^-2