
n=3k+4, k≥0 aₙ=3^3^k
in corrispondenza
k=0, n=4
a₄=3
k=1, n=7,
a₇=3³=27
k=2, n=10,
a₁₀=3^3^2=19683
k=3, n=13
a₁₃=3^3^3
....
dimostrazione:
Detto
b=³√3
a₁=b
a₂=bᵇ
a₃=(bᵇ)ᵇ=(b)^(b^2)
.......
aₙ=(b)^(b^(n-1))
Introducendo
b=3^(1/3)
aₙ=(3^(1/3))^3^((n-1)/3)
aₙ=3^(3^((n-1)/3)/3)
aₙ=3^(3^((n-1)/3-1))
aₙ=3^3^(n-4)/3
Imponendo
(n-4)/3=k≥0
k∈ℕ∪{0}
n=3k+4
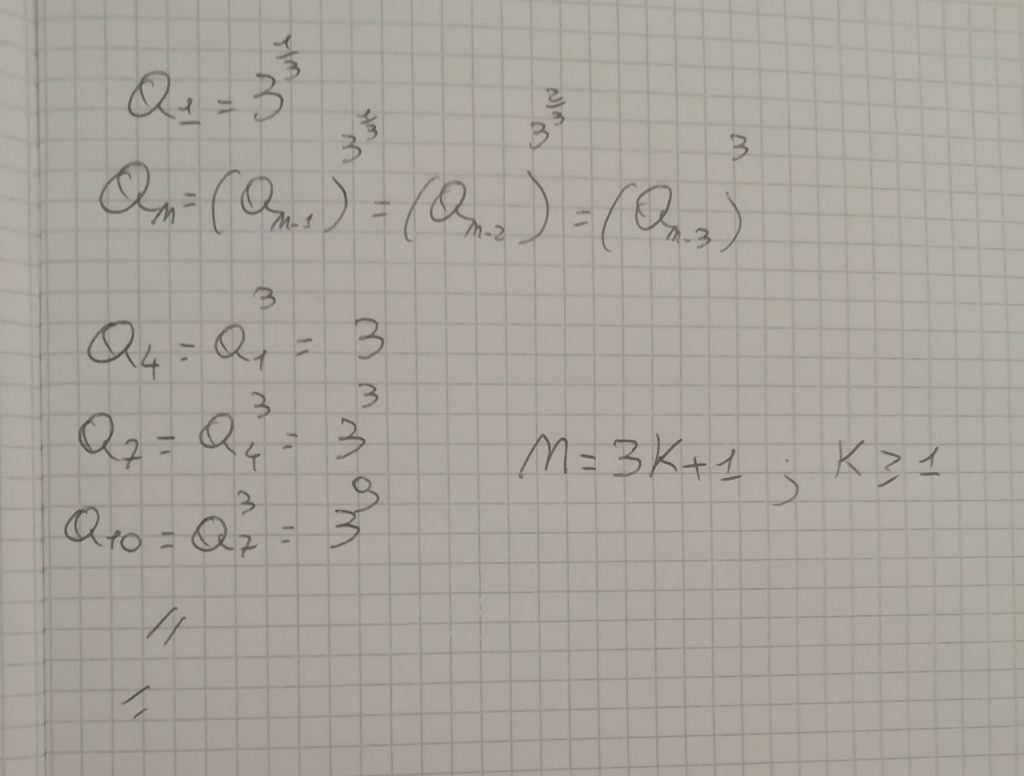
n=3 k+1 con k=1,2,3,...,n
Simbologicamente:
Detto
b=³√3
a₁=b
a₂=bᵇ
a₃=(bᵇ)ᵇ=(b)^(b^2)
.......
aₙ=(b)^(b^(n-1))
Introducendo
b=3^(1/3)
aₙ=3^(n-4)/3
Imponendo
(n-4)/3=k≥0
k∈ℕ∪{0}
n=3k+4