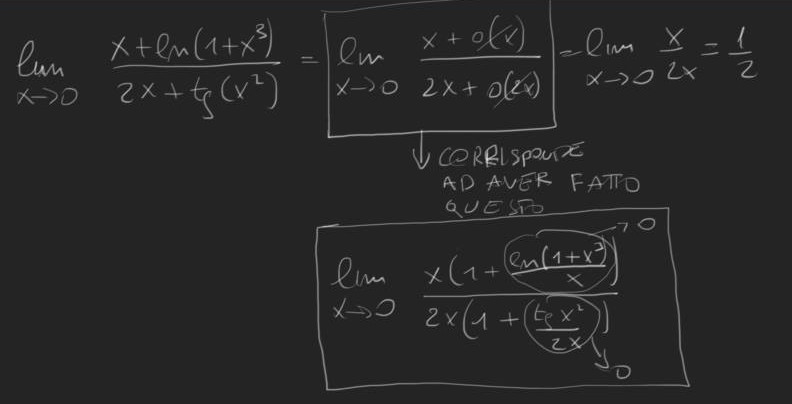

tipo: f(x)+g(x) questa posso scriverla così : f(x) + o(f(x)).
Quindi in genere togliere o(f(x)) e proseguire i calcoli usando solo f(x)
Direi che la regola fondamentale è che gli o-piccoli si possono trascurare solo in prodotti, frazioni e potenze.
[f(x)+o(f(x))] · [g(x) + o(g(x))] ~ f(x) · g(x);
[f(x)+o(f(x))] / [g(x) + o(g(x))] ~ f(x) / g(x);
[f(x)+o(f(x))]ᵃ ~ [f(x)]ᵃ (se a non dipende da x)
Se F è una funzione, in generale NON è vero che F[f(x)+o(f(x))] ~ F[f(x)] come indicato dall'esempio che hai presentato con l'esponenziale (F(x) = eˣ).
L'equazione F[f(x)+o(f(x))] ~ F[f(x)] funziona a volte... per cui uno è pensato a pensare che valga in generale, ma non è vero. Sinceramente, non so dare delle condizioni
Per esempio, per x → +∞, ln(x+x²) = ln(x²+o(x²)) ~ ln(x²), ma ln(1+1/x) = ln(1+o(1)) NON è asintotico a ln(1) = 0.