L’area del triangolo isoscele
A = B x h / 2
Mi trovo l’altezza con teorema di Pitagora triangolo rettangolo (isoscele/2)
C^2 = a^2 + b^2
Quindi 7^2 = 3,5^2 + b^2
49 = 12,25 + b^2
49-12,25 = 36,75
Radice quadra di 36,75= 6,06 arrotondo (6)
Quindi Area = 7 x 6 /2 = 21 palline..
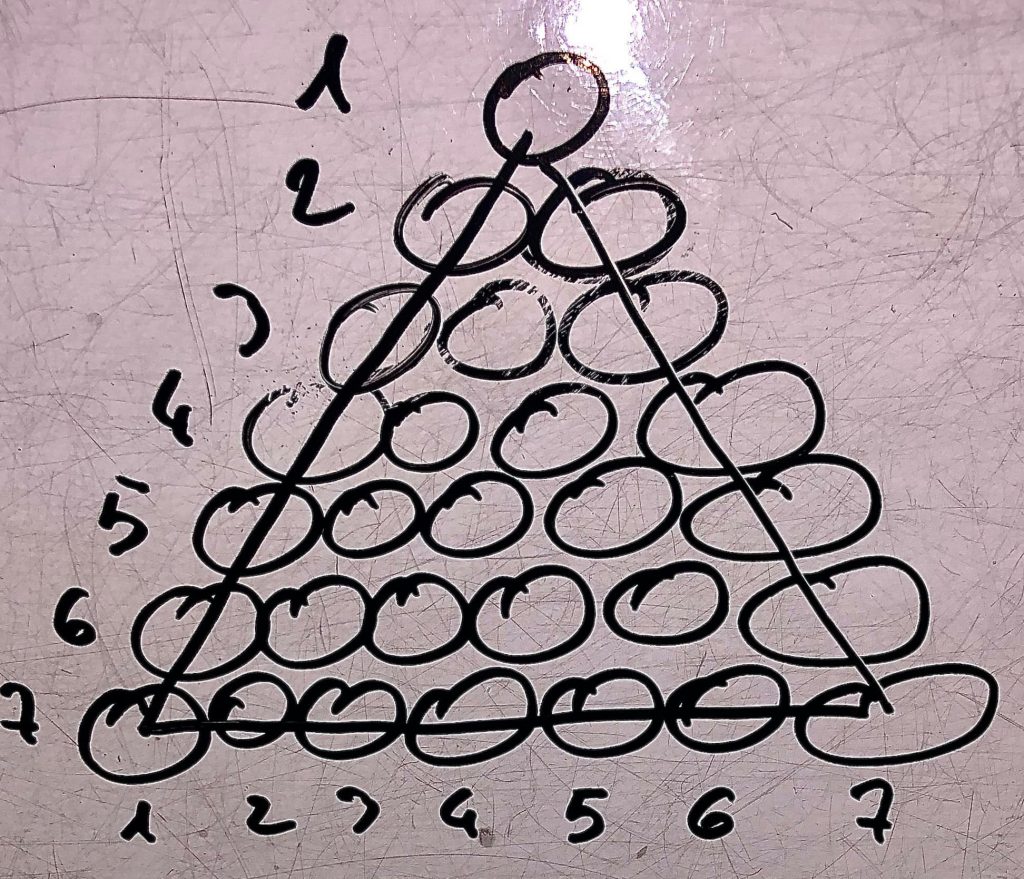
La formula è n(n+1)/2. Ci si può arrivare così.
1 + 2 + … + n-1 + n +
n + n-1 + … + 2 +1 =
=(n+1)*n (sommando verticalmente e poi orizzontalmente) ma questo è il doppio della somma. Quindi la somma è n(n+1)/2. È anche detto "teorema di Gauss bambino" perché Gauss, secondo un aneddoto, lo usò per sommare i numeri da 1 a 100, esercizio dato come punizione dalla maestra, in breve tempo.
serie aritmetica. Si deve fare la somma degli interi da 1 a 7 che è 7(1+7)/2=28.
Per calcolare il valore della somma, propongo questo procedimento, che spero sia ispirato dal testo del problema. Per prima cosa... cambio i cerchi in quadratini, perché è più facile calcolare le aree (si veda la nota in fondo al mio commento però).
L'area della figura è pari al numero totale dei quadratini (quel che vogliamo trovare). Quanto vale l'area? Bisogna sommare le aree gialla e rossa. La regione gialla è un triangolo, per cui la sua area è naturalmente base×altezza/2, in questo caso 7×7/2. Poi bisogna aggiungere i "bordi" rossi. Ciascun triangolino rosso misura 1/4, e ne abbiamo 7 per parte, cioè 7×2, in tutto quindi l'area rossa vale 7×2/4. In totale, l'area vale:
7×7/2 + 7/2 = 7×8/2 = 28.
Questo procedimento si può generalizzare, se si hanno N quadratini, il loro numero è pari a N×(N+1)/2 (è una derivazione alternativa della formula del piccolo Gauss).
Nota: se invece dei quadratini si usassero dei cerchi, la geometria del problema diventa più complicata, perché i cerchi lasciano dei buchi (di cui bisogna tenere conto) e l'altezza totale del triangolo non sarà pari a 7. Mi pare che il cambio dei cerchi in quadratini risolva comunque il problema proposto.