
Usando il teorema del coseno:
a² = b² + c² - 2bc·cos(𝛼);
b² = a² + c² - 2ac·cos(𝛽);
c² = a² + b² - 2ab·cos(𝛾).
Sommando queste tre equazioni:
a² + b² + c² = 2a² + 2b² + 2c² - 2bc·cos(𝛼) - 2ac·cos(𝛽) - 2ab·cos(𝛾),
da cui:
2bc·cos(𝛼) + 2ac·cos(𝛽) + 2ab·cos(𝛾) = a² + b² + c².
Valgono le seguenti relazioni:
𝛿 = 𝜋 - 𝛼;
𝜀 = 𝜋 - 𝛽;
𝜁 = 𝜋 - 𝛾.
Usando ancora il teorema del coseno e l'identità cos(𝜋 - x) = -cos(x):
d² = b² + c² - 2bc·cos(𝛿) = b² + c² + 2bc·cos(𝛼)
e² = a² + c² - 2ac·cos(𝜀) = a² + c² + 2ac·cos(𝛽)
f² = a² + b² - 2ab·cos(𝜁) = a² + b² + 2ab·cos(𝛾)
d² + e² + f² = 2(a² + b² + c²) + 2bc·cos(𝛼) + 2ac·cos(𝛽) + 2ab·cos(𝛾) = 3(a² + b² + c²).
Quindi per finire:
(d² + e² + f²) / (a² + b² + c²) = 3.
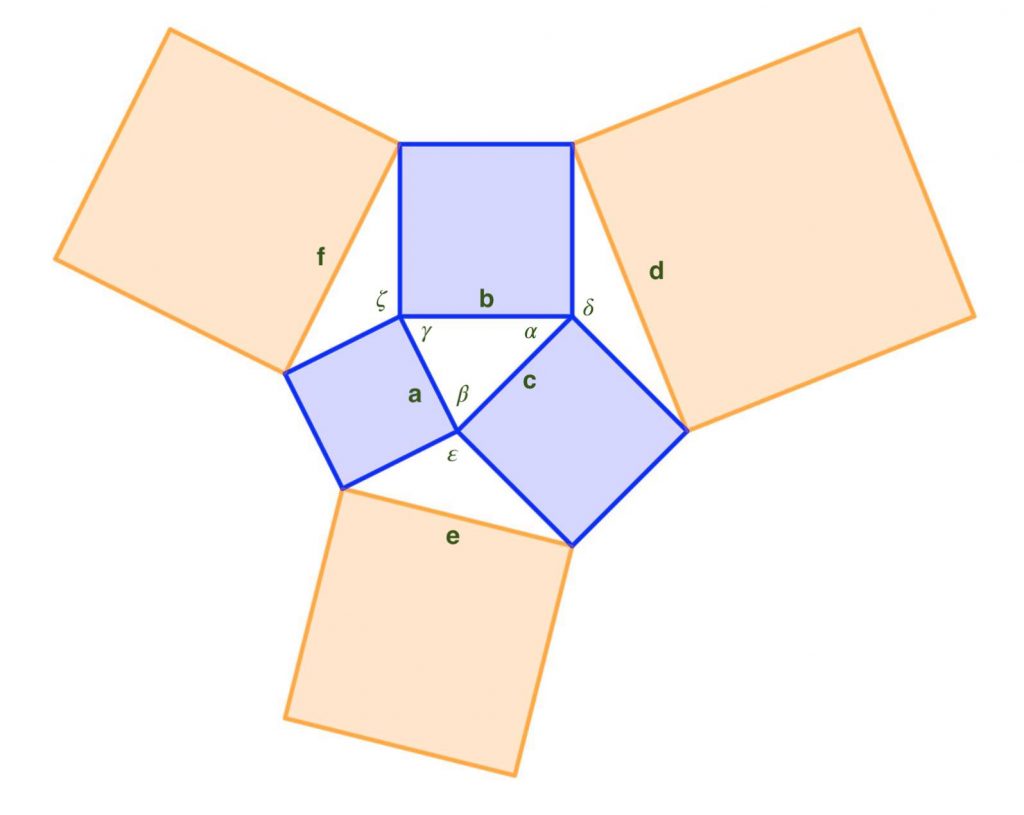
Imponendo (furbescamente) il vincolo aggiuntivo che il triangolo sia equilatero di lato L, il lato dei quadrati grandi viene L radice 3. Quindi il rapporto tra le aree viene 3