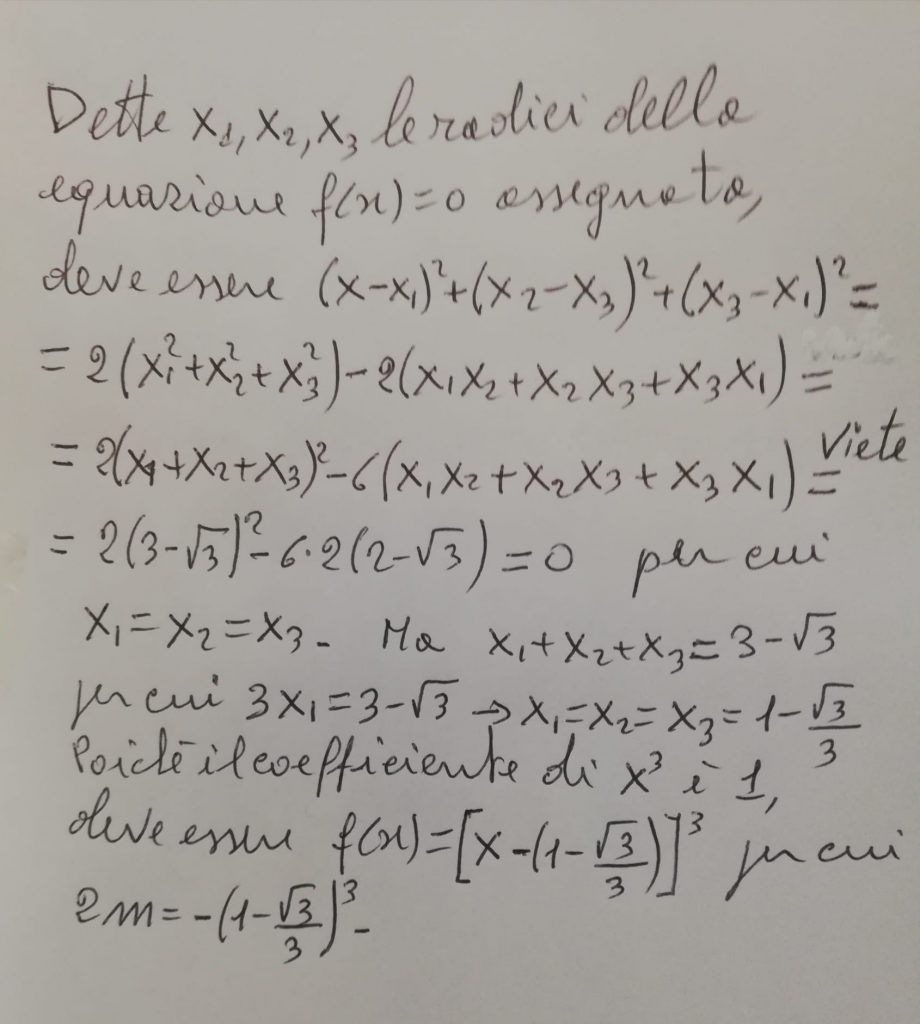potrebbe anche essere una soluzione:
3b = 3 -√3 ---> b = 1 - √3/3 --->
b² = 1 - 2√3/3 + 1/3 = 4/3- 2√3/3
3b² = 4 - 2√3 = 2(2 - √3)
x³ -3bx² + 3b²x - b³ + 2m = - b³
(x - b)³ + 2m = - b³
x = ³√( -b³ - 2m) + b con b = 1 - √3/3
potremmo anche:
x1=x2=x3= 1 - sqrt(3)/3
La derivata prima si annulla in un solo punto x= x1 = 1 - sqrt(3)/3 di conseguenza
f'(x) = a(x-x1)^2, quindi
f(x) = (a/3)(x - x1)^3 + k
visto che il coefficiente di x^3 è 1, a/3= 1
f(x) = (x-x1)^3 + k
che ha tre radici reali solo e k=0, e in tal caso si ha
x = x1 (molteplicità 3)
m non va via, ha un particolare valore reale, per determinarlo basta ricordare che 2m è il termine noto dello sviluppo (x-x1)^3
2m = (-x1) ^3
x³-(3-√3)x²+3(2-√3)x+2m=0
Δ(x)=108abcd-4b³d+b²c-4ac³-27a²d²≥0
27m²-(30√3-54)m-30√3+52≤0
al piu è nullo per
m*=5/(3√3)-1
per cui essendo
b²=3ac=6(2-√3)
la teoria impone che le radici siano una di molteplicità 3 reale
x₁=x₂=x₃=-b/(3a)=1-1/√3
dove le soluzioni, dipendono da m
ma m è obbligato ad assumere quel particolare valore per avere discriminante nullo o al più negativo. Essendo l'unico valore di m reale che da soluzioni reali quello per cui il delta è nullo le soluzioni son tutte reali nel caso e dipendono da quel valore di m*. Essendo poi b^2=3ac le soluzioni sono anche coincidenti e valgono quanto scritto, x=-b/(3a)