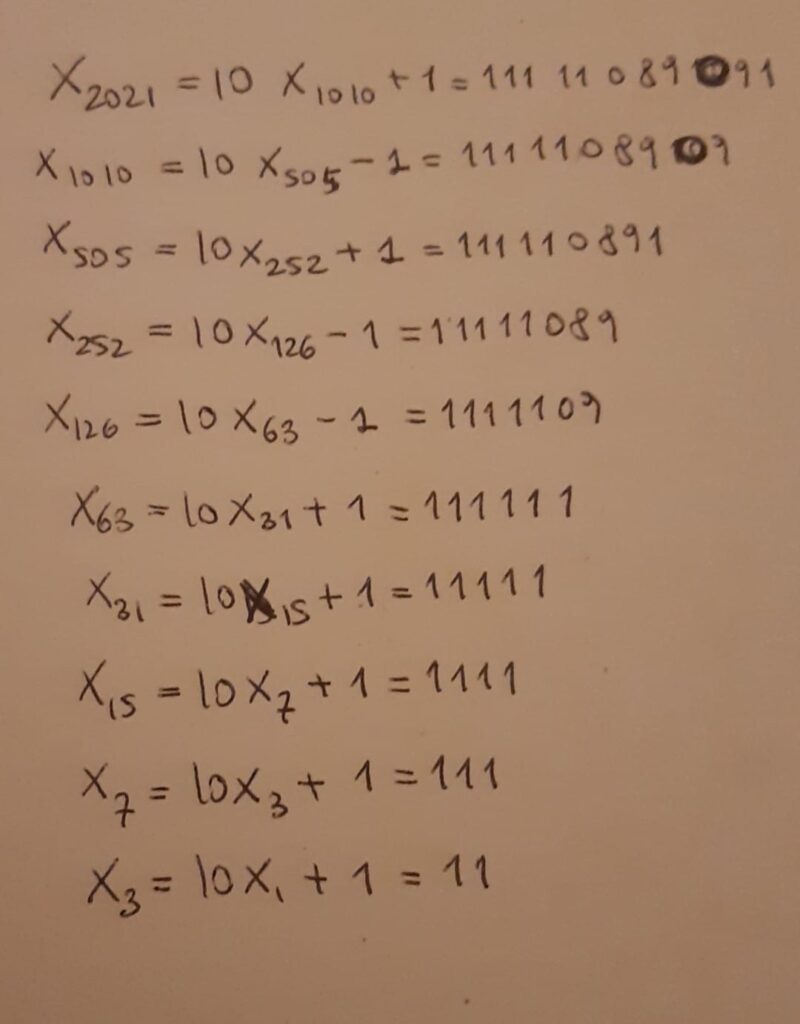Sapendo che 1 è l'elemento più piccolo dell'insieme X e che, per ogni x intero positivo, se x appartiene a X, allora apparterranno anche 10x-1 e 10x + 1, qual è l'elemento 2021esimo più grande di questo insieme X?
X = {1, 9, 11, 89, 91, 109, 111, 889, 891, 909, 911 ...}
Si procede per sostituzione a ritroso da x_2021 a x_1 e poi si risale di nuovo ad x_2021 notando che il k-esimo dispari è il numero 2k-1 e il k-esimo pari è il numero 2k. Quindi 2021 è il 1011 elemento dispari della successione e si nota che in generale:
x_{2k-1} = 10*x_{k-1} + 1
x_{2k} = 10*x_{k} - 1
Per ogni k maggiore o uguale a 1
PS: assumendo x_0 = 0