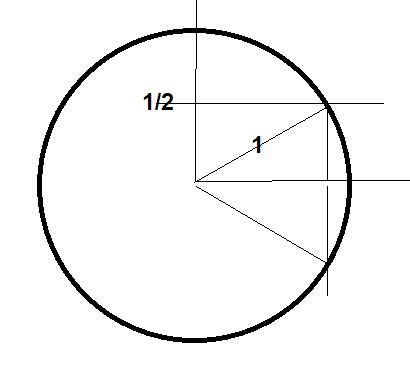
Basta chiedersi per quali angoli x il seno vale -½. Innanzitutto individuiamo gli angoli principali il cui seno è ½, ovvero secondo la teoria si può dimostrare che sono a 30° e 150°, in radianti π/6 e 5/6π Individuato ciò, ricordando che il seno è l'ordinata del segmento associato all'angolo, esso è negativo nel terzo e quarto quadrante: ovvero, valutando in senso orario, al sen(-π/6)=-sen(π/6)=-½ ; e in senso anti-orario al sen(π+π/3)=-sen(π/3)=-½ , sapendo che il seno di un angolo qualsiasi sommato ad un angolo piatto, coincide col seno dell'angolo stesso, ma negativo capitando nel terzo quadrante.
Perciò l'equazione è soddisfatta per tutti gli angoli x=-π/6 + 2kπ (-π/6 equivalentemente è 11/6π valutando in senso anti-orario la prima tranche di soluzioni); e x=π+π/6 + 2kπ = 7/6 π +2kπ. Con la relativa periodicità, affermando che la funzione si ripete ogni 360° ottenendo infinite soluzioni dipendenti dal parametro k∈ℤ
Considera la circonferenza trigonometrica.
Se l'altezza è metà della circonferenza, beh, se prolunghi il lato (1/2) ottieni un equilatero, i cui angoli è noto sono 60°.
Essendo la metà è 30°.
Per averlo in radianti vai la proporzione solita
2Pi:360=x:30 e ottieni Pi/6