
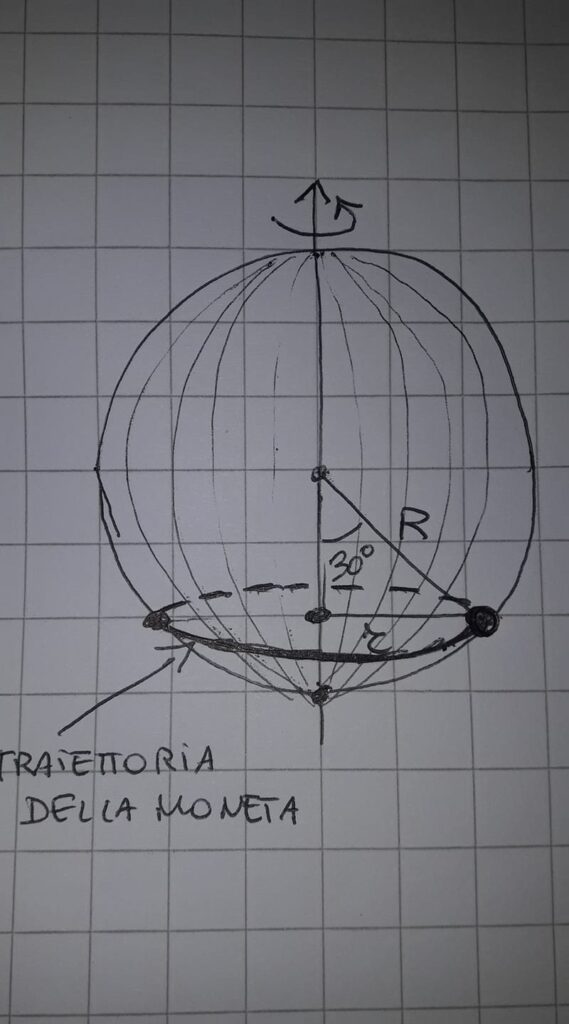
sulla guida agisce la forza centripeta m*omega^2*r (dove r=R*sen(theta); sulla rondella quindi agisce l'opposto di questa forza; la componente di questa forza, normale alla guida circolare è la reazione vincolare della guida; la componente verticale invece uguaglia il peso della rondella (se 30° è una posizione di equilibrio)
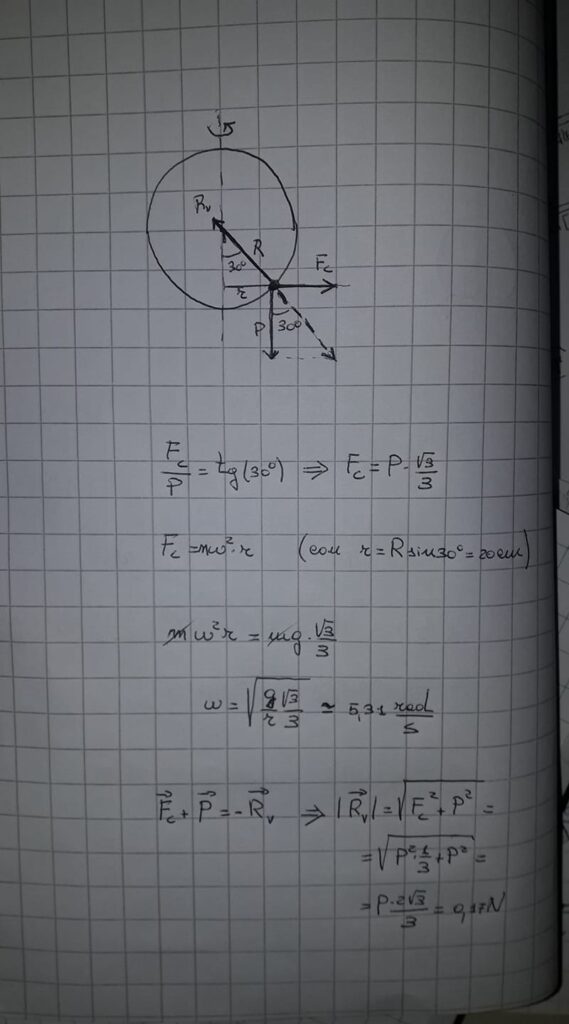
se la rondella si sposta di poco dalla posizione di equilibrio, sarà sottoposta ad una piccola forza centrifuga. La reazione vincolare è il vettore opposto al vettore verde in figura, mentre la rondella è sottoposta alla forza Fc + P. La somma delle tre forze non è più zero, la componente non equilibrata è il vettore rosso in figura, direzione parallela alla tangente alla circonferenza; la moneta "sale".
Scomponendo il vettore P + Fc in una direzione parallela alla tangente ed una perpendicolare, la componente parallela è rivolta verso il basso! (L'opposto del vettore rosso in figura) dunque la rondella scende, la posizione ad angolo zero a quanto pare è una posizione di equilibrio STABILE.
lo schema te ne rendi conto. Se la posizione della rondella è vicina a theta = 0, la forza centrifuga tende a zero, dunque Fc + P è circa uguale a P. La reazione vincolare bilancia la componente perpendicolare alla tangente, la componente parallela rimane non bilanciata, e la rondella si riporta nella posizione di equilibrio!!! È esattamente la stessa cosa di una pallina sospesa ad un filo che viene leggermente allontanata dalla posizione di equilibrio
scrivi l'energia meccanica del sistema in un riferimento rotante, poi guarda cosa succede al variare di omega. Vedrai che esiste una velocità critica per cui si rompe una simmetria e succede una magia: dove c'era un minimo nasce un massimo e due minimi simmetrici si incamminano verso +/- pi/2, meta che non raggiungeranno mai. Sicuramente, un esercizio molto istruttivo.